GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
This topic is relevant for:

How To Calculate Surface Area
Here we will learn how to calculate the surface area of a variety of three-dimensional shapes, including cuboids, prisms, cylinders, cones and spheres.
There are also surface area worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is surface area?
The surface area of a three dimensional shape is the total area of all of the faces.
To find the surface area of a shape, we find the area of each face and add them together.
E.g.
| Face | Area |
| Front | ½ × 4 × 3 = 6 |
| Back | 6 |
| Bottom | 4 × 6 = 24 |
| Top | 5 × 6 = 30 |
| Left side | 3 × 6 = 18 |
Total surface area
\begin{aligned} &= 6+6+24+30+18 \\ &=84cm^2 \end{aligned}The measurements here are in centimetres so the surface area is measured in square centimetres (cm^2) .
What is surface area?

How to calculate surface area
In order to calculate surface area:
- Calculate the area of each face.
- Add the areas together.
- Write the answer, including the units.
Explain how to calculate surface area

Surface area worksheet

Get your free surface area worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Surface area worksheet

Get your free surface area worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on 3D shapes
How to calculate surface area is part of our series of lessons to support revision on 3D shapes. You may find it helpful to start with the main 3D shapes lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Surface area examples
Example 1: surface area of a cuboid
Work out the surface area of the cuboid. We can think of this as finding the surface area of a rectangular prism or the surface area of a box.
- Calculate the area of each face.
| Face | Area (cm2) |
| Front | 10 × 4 = 40 |
| Back | 40 |
| Bottom | 10 × 6 = 60 |
| Top | 60 |
| Left side | 6 × 4 = 24 |
| Right side | 24 |
2Add the areas together.
The sum of the areas is: 40+40+60+60+24+24=248
3Write the answer, including the units.
The measurements are in cm so the surface area will be measured in cm^2 .
Total surface area = 248cm^2
Example 2: surface area of a cube
Work out the surface area of the cube:
Calculate the area of each face.
Since it is a cube, all of the faces are the squares and of equal size.
Area of a square formula: \text{(side length)}^2
So, the area of each face =9 \times 9=81cm^2
Add the areas together.
There are 6 faces, each with an area of 81cm^2
6 \times 81=486
Write the answer, including the units.
The measurements of the cube are in cm so the area will be measured in cm^2
Total surface area = 486cm^2
Example 3: surface area of a triangular prism
Work out the surface area of the triangular prism
Calculate the area of each face.
| Face | Area (cm2) |
| Front | ½ × 12 × 8 =48 |
| Back | 48 |
| Bottom | 12 × 7 = 84 |
| Left side | 10 × 7 = 70 |
| Right side | 70 |
Add the areas together.
48+48+84+70+70
Write the answer, including the units.
The units are in mm so the area will be measured in mm^2
Surface area = 320mm^2
Example 4: surface area of a cylinder
The radius of this cylinder is 5m and the height of the cylinder is 2m. Work out the surface area of the cylinder. Give your answer to 3 significant figures.
Calculate the area of each face.
As the area of each face includes the value of \pi , leave the area of each face in terms of \pi , then we can add them together more easily.
\begin{aligned}
\text{Curved surface area (lateral surface area)}&=2 \pi rh\\\\
&=2 \times \pi \times 5 \times 2\\\\
&=20\pi
\end{aligned}
The cross section is a circle.
\begin{aligned} \text{Area of circle }&=\pi r^{2}\\\\ &=\pi \times 5^{2}\\\\ &=25\pi \end{aligned}
The base is the same as the top so the area of the base is also 25\pi .
Add the areas together.
20\pi+25\pi+25\pi=70\pi
70\pi=219.9114858...
Write the answer, including the units.
We need to round the answer to 3 significant figures.
Surface area = 220m^2 \; (3sf)
Example 5: surface area of a cone
Work out the surface area of the cone. Give your answer to 1 decimal place.
Calculate the area of each face.
Similar to the cylinder, the area of each face of the cone is calculated using \pi . To avoid any rounding errors, keep the answer in terms of \pi , then round the answer at the very end of the calculation.
\begin{aligned} \text{Curved surface area }&=\pi rl\\\\ &=\pi \times 5 \times 13\\\\ &=65\pi \end{aligned}
Notice that we use the slant height of the cone, not the vertical height.
The base is a circle so the area of the base = \pi r^2
\begin{aligned} \text{Area of a circle }&=\pi r^{2}\\\\ &=\pi \times 5^{2}\\\\ &=25\pi \end{aligned}
Add the areas together.
65\pi+25\pi=90\pi
90\pi=282.7433388...
Write the answer, including the units.
We need to write the answer to 1 decimal place.
Total surface area = 282.7cm^2 \; (1dp).
Example 6: surface area of a sphere
Work out the surface area of the sphere. Give your answer to the nearest integer.
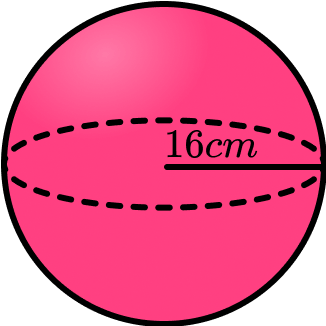
Calculate the area of each face.
The surface area formula for a sphere is:
\begin{aligned} \text{Surface area }&=4 \pi r^{2}\\\\ &=4 \times \pi \times 16^{2}\\\\ &=3216.9908… \end{aligned}
Add the areas together.
A sphere only has one face.
Write the answer, including the units.
We need to write our answer to the nearest integer.
Surface area = 3217cm^2
Common misconceptions
- Calculating with different units
You need to make sure all measurements are in the same units before calculating surface area. (For example you can’t have some measurements in cm and some in m ).
- Make sure you have the correct units
For area we use square units such as cm^2 (square centimetres), m^2 (square metres), in^2 (square inches) and ft^2 (square feet),
For volume we use cube units such as cm3, \; m^3, \; km^3
- Calculating volume instead of surface area
Volume and surface area are different things – volume tells us the space within the shape whereas surface area is the total area of the faces. To find surface area, work out the area of each face and add them together.
- Rounding
It is important to not round decimals until the end of the calculation. Rounding too early will result in an inaccurate answer. Keep as many values in terms of \pi until you need to calculate the final rounded answer.
Practice surface area questions
1. Find the surface area of the rectangular prism below.
92cm^2

48cm^2

108cm^2

76cm^2

Calculating the area of each face, we have:
| Face | Area (cm2) |
| Front | 8 × 2 =16 |
| Back | 16 |
| Bottom | 8 × 3 = 24 |
| Top | 24 |
| Left side | 2 × 3 = 6 |
| Right side | 6 |
Total surface area: 16+16+24+24+6+6=92cm^2
2. Calculate the surface area of the triangular prism.
360cm^2

240cm^2

300cm^2

480cm^2

Calculating the area of each face, we have:
| Face | Area (cm2) |
| Front | ½ × 5 × 12 =30 |
| Back | 30 |
| Bottom | 8 × 12 = 96 |
| Top | 8 × 13 = 104 |
| Left side | 8 × 5 = 40 |
Total surface area = 30+30+96+104+40=300cm^2
3. Work out the surface area of the prism.
464mm^2

432mm^2

400mm^2

440mm^2

Calculating the area of each face, we have:
| Face | Area (cm2) |
| Front | ½(2 + 8) × 4 =20 |
| Back | 20 |
| Bottom | 8 × 20 = 160 |
| Top | 2 × 20 = 40 |
| Left side | 5 × 20 = 100 |
| Right side | 100 |
Total surface area = 20+20+160+40+100+100=440mm^2
4. Find the surface area of the cylinder. Give your answer to 3 significant figures.
1190m^2

633m^2

449m^2

346m^2

\begin{aligned}
\text{Curved surface area }&=2 \pi rh\\\\
&=2 \times \pi \times 6.5 \times 9\\\\
&=117\pi
\end{aligned}
\begin{aligned}
\text{Area of a circle }&=\pi r^{2}\\\\
&=\pi \times 6.5^{2}\\\\
&=\frac{169}{4}\pi
\end{aligned}
Total surface area: 117\pi+\frac{169}{4}\pi+\frac{169}{4}\pi=\frac{403}{2}\pi
\frac{403}{2}\pi=633.0309197…
Surface area = 633m^2 \; (3sf)
5. Work out the surface area of the cone. Give your answer to 3 decimal place.
29.5cm^2

22.6cm^2

7.5cm^2

23.9cm^2

\begin{aligned}
\text{Curved surface area }&=\pi rl\\\\
&=\pi \times 2 \times 2.7\\\\
&=5.4\pi
\end{aligned}
\begin{aligned}
\text{Area of a circle }&=\pi r^{2}\\\\
&=\pi \times 2^{2}\\\\
&=4\pi
\end{aligned}
Total surface area: =5.4\pi+4\pi=9.4\pi
Surface area = 29.5cm^2 \; (1dp)
6. Calculate the surface area of the sphere. Give your answer to 2 decimal place.
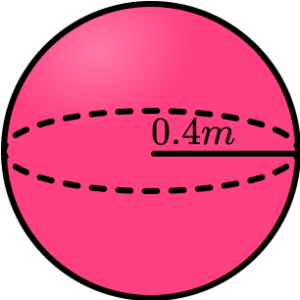
201.06m^2

2.01m^2

0.27m^2

25.27m^2

\begin{aligned}
\text{Surface area of a sphere }&=4 \pi r^{2}\\\\
&=4 \times \pi \times 0.4^{2}\\\\
&=0.64\pi \\\\
&=2.010619298…
\end{aligned}
Surface area = 2.01m^2 \; (2dp)
Surface area GCSE questions
1. Calculate the surface area of the cone. Give your answer to the nearest integer.
(4 marks)
\begin{aligned}
\text{Curved surface area }&=\pi \times 21 \times 37\\\\
&=2441.017492…\text{ or }777\pi
\end{aligned}
(1)
\begin{aligned}
\text{Area of circle }&=\pi \times 21^{2}\\\\
&=1385.4423…\text{ or }441\pi
\end{aligned}
(1)
\text{Total surface area } = \text{their }777\pi+ \text{their } 441\pi =1218\pi =3826.459852…
(1)
\text{Surface area } = 3826cm^2
(1)
2. A drinks company is designing a new product. Can A has a volume of 108\pi \text{ cm}^3 and Can B has a volume of 98\pi \text{ cm}^3.
The company wants to minimise their packaging for the new product. Which should they choose? Explain your answer.
(9 marks)
Can A
\begin{aligned}
\text{Curved surface area }&=2 \times \pi\times 3 \times 12\\\\
&=226.1946711…\text{ or }72\pi
\end{aligned}
(1)
\begin{aligned}
\text{Area of circle }&=\pi \times 3^{2}\\\\
&=28.27433388…\text{ or }9\pi \end{aligned}
(1)
\text{Total surface area: }\text{their }72\pi+(2\times\text{their }9\pi)=90\pi=282.7433388…
(1)
Can B :
\begin{aligned}
\text{Curved surface area }&=2 \times \pi\times 3.5 \times 8\\\\
&=175.9291886…\text{ or }56\pi \end{aligned}
(1)
\begin{aligned}
\text{Area of circle }&=\pi \times 3.5^{2}\\\\
&=38.48451001…\text{ or }12.25\pi \end{aligned}
(1)
\text{Total surface area: }\text{their }56\pi+(2\times\text{their }12.25\pi)=80.5\pi=252.8982086…
(1)
Volume to Surface Area ratio for Can A
\begin{aligned}
&108 \pi :90 \pi \\\\
&=1:0.83 \end{aligned}
(1)
Volume to Surface Area for Can B
\begin{aligned}
&98 \pi :80.5 \pi \\\\
&=1:0.82 \end{aligned}
(1)
They should use can B because it has a smaller volume to surface area ratio.
(1)
3. The surface area of this sphere is 200cm^2. Calculate the radius of the sphere. Give your answer to 3sf.
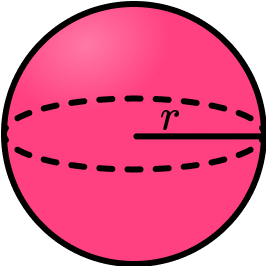
(4 marks)
4\pi r^{2}=200
(1)
r^{2}=\frac{200}{4\pi}=15.91549431…
(1)
r=\sqrt{15.91549431…}=3.989422804…
(1)
r=4.00cm \; (3sf)
(1)
Learning checklist
You have now learned how to:
- Find the surface area of cuboids and prisms
- Find the surface area of cylinders, cones and spheres
- Use the properties of faces, surfaces, edges and vertices of cubes and cuboids to solve problems in 3D
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.