1. Which of these shapes show an equilateral triangle?

Triangles

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Lines of symmetry Rotational symmetry Types of angles Angles on a straight line Angles in a triangle How to work out perimeter

This topic is relevant for:

GCSE Maths Geometry and Measure 2D Shapes Polygons

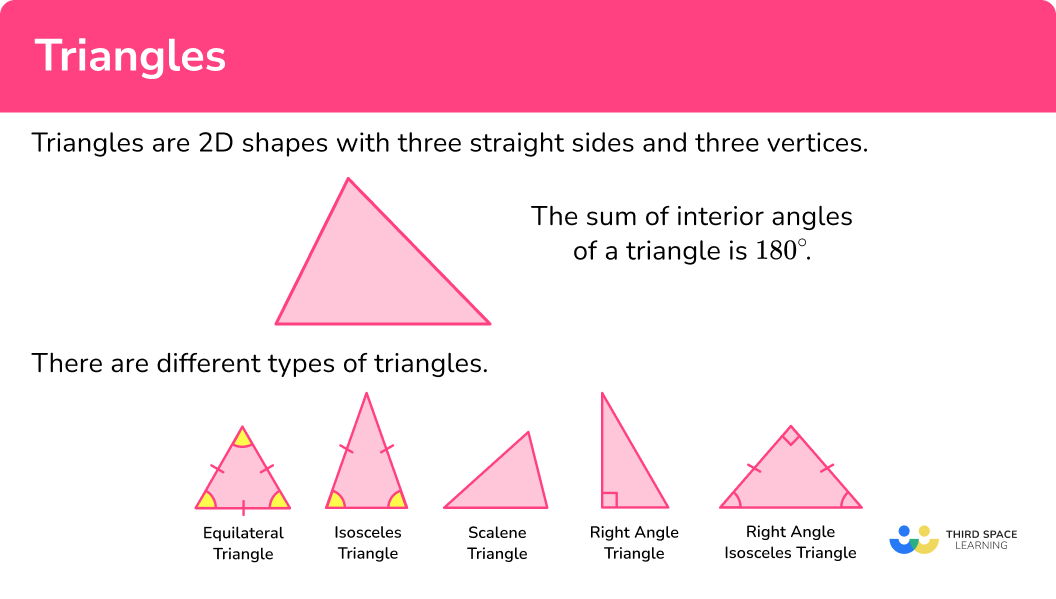
Triangles

Here we will learn about triangles, including what a triangle is and how to solve problems involving their sides and their angles.

There are also triangles worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are triangles?

Triangles are 2D shapes with three straight sides and three vertices. These are the only two key properties of triangles.

To solve problems involving triangles, we need to be able to gather information about its side lengths and/or its interior angles and apply these to the problem.

The sum of interior angles of a triangle is $\bf{180°}.$

For example,

29^{\circ}+68^{\circ}+83^{\circ}=180^{\circ}.

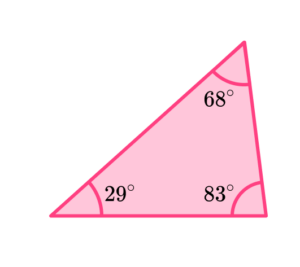
If a triangle’s angles are all acute angles (less than $90^{\circ}$ ), it is sometimes known as an acute triangle.

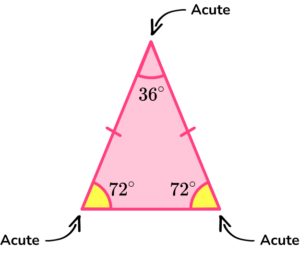
If a given triangle has one obtuse angle it is sometimes known as an obtuse triangle.

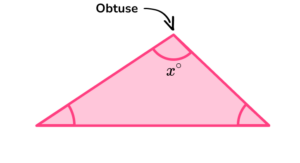
Step-by-step guide: Angles in a triangle

What are triangles?

Types of triangles

There are different types of triangles that have different properties.

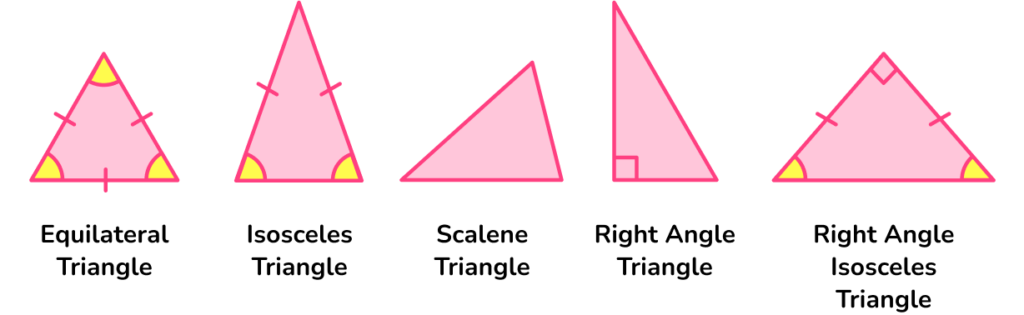
Being able to recognise different types of triangles is known as classifying triangles.

Step-by-step guide: Types of triangles

Equilateral triangles

An equilateral triangle has the following properties,

All sides are equal length.
All angles are equal size $(60^{\circ})$ .

An equilateral triangle has $3$ lines of symmetry. The lines go from one vertex to the middle of the opposite side.

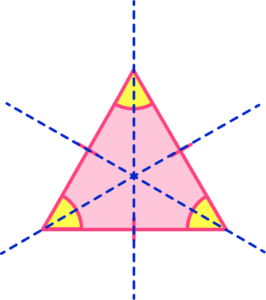
The lines of symmetry are angle bisectors of the vertices and are also perpendicular bisectors of the sides of the equilateral triangle.

Step-by-step guide: Equilateral triangles

Isosceles triangles

An isosceles triangle has the following properties,

Two sides are equal length.
Two equal angles.

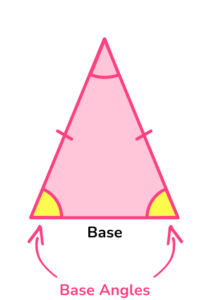
The two equal angles are called base angles and they are opposite the sides of equal length. The unequal side is known as the base and is opposite the unequal angle.

Step-by-step guide: Isosceles triangles

Scalene triangles

A scalene triangle has the following properties,

No equal sides.
No equal angles.

Step-by-step guide: Scalene triangles

Right-angled triangles

A right-angled triangle has the following property,

One right angle.

The longest side of a right-angled triangle is opposite the right-angle. It is called the hypotenuse.

The Pythagorean theorem is used to determine missing side lengths of a right-angled triangle. If a question involves both the sides of the triangle and one of the angles, we could use trigonometry.

A special case of a right-angled triangle is a right-angled triangle which also has two equal sides. It can be known as an isosceles right triangle or an isosceles right-angled triangle. The two equal angles will both be $45^{\circ}.$

Step-by-step guide: Right angle triangle

Area of a triangle

The area of a triangle can be found by using the formula,

$A=\frac{1}{2}bh$ ,

where $b$ is the base length and $h$ is the perpendicular height of the triangle.

Sometimes these values need to be calculated.

The area of a triangle is given in square units.

Step-by-step guide: Area of a triangle

Impossible triangles

It is impossible for a triangle to contain more than one obtuse angle as the sum of angles in a triangle is $180^{\circ}.$

For example,

A triangle contains the three angles $98^{\circ}, \ 91^{\circ}$ and $5^{\circ}.$
This gives us the angle sum of $98+91+5=194^{\circ}$ and so as angles in a triangle always total $180^{\circ}.$ This is an impossible triangle.

A triangle contains two right angles, and a third angle $x^{\circ}.$
The sum of angles in the triangle is therefore $90+90+x=(180+x)^{\circ}.$
The value of $x$ must equal $0$ for the angles to add to $180^{\circ}$ and so this is another impossible triangle.

How to answer questions involving triangles

In order to solve problems involving triangles:

Locate known angles and calculate any necessary unknown angles.
Locate known sides and calculate any necessary unknown side lengths.
Solve the problem using any necessary values.

Explain how to answer questions involving triangles

Types of triangles worksheet

Get your free triangles worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Types of triangles worksheet

Get your free triangles worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Triangles examples

Example 1: calculate the missing angle in an isosceles triangle

Find angle $x.$

Locate known angles and calculate any necessary unknown angles.

This problem involves the internal angles of a triangle. The sum of interior angles of a triangle is $180^{\circ}.$ One angle is given.

As two sides have a dash through them indicating they are the same length, the triangle is isosceles and so the triangle contains the two base angles $63^{\circ}$ and $63^{\circ}.$

2Locate known sides and calculate any necessary unknown side lengths.

As we need to determine the size of angle $x$ and we have information about the other two angles, we can use these to find the missing angle. We do not need to calculate any length of the triangle.

3Solve the problem using any necessary values.

Using the two known angles and the angle fact that the sum of angles in a triangle is $180^{\circ},$

180-(2\times 63)=54.

Therefore angle $x=54^{\circ}.$

Example 2: finding the missing angle including external angles

Determine the size of angle $x.$

Locate known angles and calculate any necessary unknown angles.

This problem involves the interior and exterior angles of a triangle. The sum of interior angles of a triangle is $180^{\circ}.$ One of the angles in the triangle is a right-angle which is $90^{\circ}.$

As the sum of angles on a straight line total $180^{\circ},$ we can find the third angle in the triangle,

$180-156=24^{\circ}.$

Labelling this onto the diagram, we now have,

The three interior angles of the triangle are $90^{\circ}, 24^{\circ}$ and $x^{\circ}.$

Locate known sides and calculate any necessary unknown side lengths.

This step is not needed for this question as we know two of the three angles within the triangle and we are finding the value of the missing angle $x.$

Solve the problem using any necessary values.

We use the angle fact that interior angles of a triangle sum to $180^{\circ}$ to work out the third angle.

$180-(90+24)=66^{\circ}$

Therefore angle $x=66^{\circ}.$

Example 3: finding the missing angle (right-angled isosceles)

Calculate the missing angle $x.$

Locate known angles and calculate any necessary unknown angles.

One of the angles in the triangle is a right-angle which is $90^{\circ}.$ As there are two sides of the triangle with a dash through them, these lines are equal in length and so we have a right-angled isosceles triangle.

This means that the remaining two angles are the same, and the three angles must total $180^{\circ}.$ The two remaining angles are therefore

$(180-90)\div{2}=90\div{2}=45^{\circ}.$

Locate known sides and calculate any necessary unknown side lengths.

We know that two sides are of equal length but we do not need to determine the length of any side of the triangle and so we can move on to step 3.

Solve the problem using any necessary values.

As adjacent angles on a straight line sum to $180^{\circ},$ we can use this to find the angle $x$ as it is on a straight line with the angle $45^{\circ}.$

$180-45=135^{\circ}$

Therefore angle $x=135^{\circ}.$

Example 4: calculating the perimeter

The sides of a triangle are $13 \ cm, 16 \ cm$ and $21 \ cm.$ What is the perimeter of the triangle?

Locate known angles and calculate any necessary unknown angles.

The angles are not involved in this question as we want to find the perimeter which is a length, and we do not know any angles in the triangle.

Locate known sides and calculate any necessary unknown side lengths.

The three sides of the triangle are given and so we have the information needed to answer the question.

Note: The sides are different lengths and so it is a scalene triangle.

Solve the problem using any necessary values.

The perimeter can be found by finding the total of the $3$ sides. We therefore add together the side lengths to get the perimeter.

$13+16+21=50\text{ cm}$

The perimeter of the triangle is $50 \ cm.$

Example 5: perimeter problem using congruent triangles

Here is a triangle.

Two of these triangles are joined on their shortest sides to make a parallelogram. Calculate the perimeter of the parallelogram.

Locate known angles and calculate any necessary unknown angles.

There is a right angle in the triangle, denoted using a square and so it is a right-angled triangle. As we want to find the perimeter of the parallelogram it produces, which is a length, we do not need to find the size of any other angle in the triangle.

Locate known sides and calculate any necessary unknown side lengths.

The three side lengths are known $(3 \ cm, 4 \ cm,$ and $5 \ cm)$ and so we can move on to step $3.$

Solve the problem using any necessary values.

The question states that “two of these triangles are joined on their shortest sides to make a parallelogram”.

The shortest side of the right-angled triangle is the perpendicular height, $3 \ cm,$ and so we need to join two of these triangles together at this side to form a parallelogram. It is useful to label each side length here.

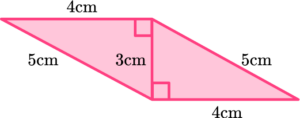
The perimeter can be found by finding the total of the sides. Remember that the $3 \ cm$ length is the perpendicular height of the parallelogram now and so it does not form part of the outside of the shape.

The perimeter is therefore the sum of the four side lengths, $4 \ cm, 5 \ cm, 4 \ cm,$ and $5 \ cm.$

$4+5+4+5=18\text{ cm}$

The perimeter of the parallelogram is $18\text{ cm}.$

Example 6: perimeter problem using ratio

The perimeter of a triangle is $119 \ cm.$

The ratio of the sides of the triangle is $5:4:8.$

Determine the length of each side of the triangle.

Locate known angles and calculate any necessary unknown angles.

The angles of the triangle are not involved in this question as we are calculating the side lengths of the triangle and have no information about the angles within the triangle.

Locate known sides and calculate any necessary unknown side lengths.

The three sides of the triangle are not given. But we have been given the ratio of the sides. Drawing a sketch of what the triangle may look like (although not essential), we have

Solve the problem using any necessary values.

Currently we have a triangle with a perimeter of $4+5+8=17 \ cm.$ As we want a similar triangle with a perimeter of $119 \ cm,$ we need to find the scale factor of enlargement. We do this by dividing the desired perimeter, by the scaled perimeter.

$119\div{17}=7$

We therefore know that each side length must be $7$ times greater than our scaled triangle. We therefore need to multiply each side length by $7.$

$5\times 7=35$

$4\times 7=28$

$8\times 7=56$

This gives us the three side lengths, $35 \ cm, 28 \ cm,$ and $56 \ cm.$

Note: This is exactly the same approach as if we were to divide a quantity into a ratio, as explained below.

We need to divide the perimeter by the total of the parts of the perimeter.

$119\div (5+4+8)=7$

We then multiply the ratio parts by $7.$

$5\times 7=35$

$4\times 7=28$

$8\times 7=56$

The lengths of the sides of the triangle are $35 \ cm, 28 \ cm,$ and $56 \ cm.$

Common misconceptions

Angles in polygons

Make sure you know your angle properties as getting these confused causes quite a few misconceptions.

◌ Angles in a triangle total $180^{\circ}$ .

◌ Angles in a quadrilateral total $360^{\circ}$ .

Angle facts

Make sure you know your angle properties.

◌ Adjacent angles on a straight line add up to $180^{\circ}$ .

◌ Vertically opposite angles are equal.

◌ Alternate angles are equal.

◌ Corresponding angles are equal.

Practice triangle questions

triangle question 1 c

An equilateral triangle has all equal sides and all equal angles.

Scalene

Equilateral

Isosceles

Right-angled

$43 \ mm$ is the same as $4.3 \ cm.$ Since two sides are the same, it is an isosceles triangle.

84^{\circ}

63^{\circ}

42^{\circ}

96^{\circ}

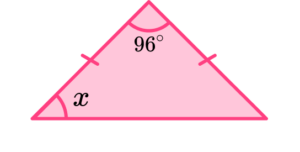
The triangle has two equal side lengths and so it is an isosceles triangle. This means that the base angles will be equal. The interior angles of a triangle sum to $180^{\circ}.$ Angle $x$ is therefore equal to

(180-96)\div 2=42^{\circ}.

Angle $x=42^{\circ}$

142^{\circ}

81^{\circ}

38^{\circ}

61^{\circ}

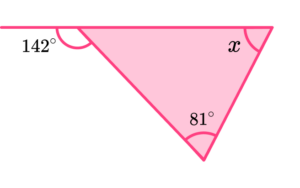
As the sum of adjacent angles is $180^{\circ},$ the angle next to $142^{\circ}$ is equal to $180-142=38^{\circ}.$

As the sum of angles in a triangle is $180^{\circ},$ the unknown value of $x$ is equal to $180-(81+38)=61^{\circ}$ and so $x=61^{\circ}.$

12 \ cm

24 \ cm

19 \ cm

14 \ cm

The two congruent triangles will make a rectangle when they are joined on their longest side (the hypotenuse).

triangle question 5 explanation

The perimeter of the rectangle will be

2\times (3+4)=14.

9 \ cm

15 \ cm

18 \ cm

12 \ cm

The ratio of the sides of the isosceles triangle would be $1:2:2.$

triangle question 6 explanation

The unequal side is the shortest side and can be found by

45\div (1+2+2)=45\div 5=9.

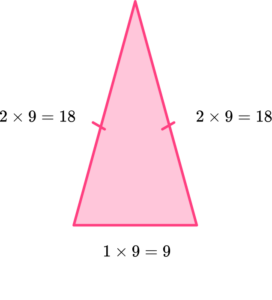
triangle question 6 explanation-1

The sides of the triangles will be $9 \ cm, 18 \ cm,$ and $18 \ cm.$ The shortest side will be $9 \ cm.$

Equilateral triangle GCSE questions

1. Here is a triangle.

Draw the line(s) of symmetry of the shape.

(2 marks)

Show answer

For one line of symmetry.

(1)

For three lines of symmetry.

(1)

2. Below is a diagram showing the triangle $ABC$ . The point $D$ lies on the line $AC$ such that $BD = CD.$

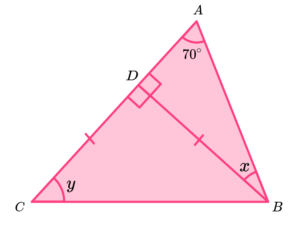
triangle GCSE question 2

(a) Determine the size of angle $x.$

(b) Find angle $y.$

(4 marks)

Show answer

(a)

180-(90+70)

(1)

20^{\circ}

(1)

(b)

(180-90)\div{2}

(1)

45^{\circ}

(1)

3. (a) Write down the coordinates of point $B.$

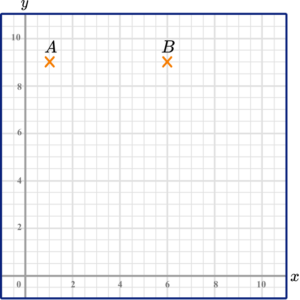
triangle GCSE question 3 a

(b) Plot the point $(1,3)$ and label it $C.$

Find the area of the triangle.

(4 marks)

Show answer

(a) $(6,9)$

(1)

(b)

triangle GCSE question 3 b

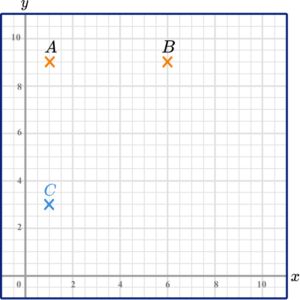
(1)

(c)

(6\times 5)\div 2

(1)

15 \ cm^2

(1)

4. The perimeter of a triangle $ABC$ is $60 \ cm.$

The ratio of the sides of the triangle are $2:3:3.$
(a) What type of triangle is $ABC$ ?

(b) Find the smallest side of the triangle $ABC.$

Heron’s formula is

\text{Area}=\sqrt{s(s-a)(s-b)(s-c)}

where $s$ is half the perimeter and $a, b$ and $c$ are the three side lengths.

Use Heron’s formula along with your solution to part b) to find the area of the triangle $ABC.$

Give your answer to $3$ significant figures.

State the units for your answer.

(8 marks)

Show answer

(a) Isosceles

(1)

(b)

60\div (2+3+3)=60\div 8 \ (=7.5)

(1)

2\times 7.5=15

(1)

(c)

s=60\div 2 (=30)

(1)

The second and third sides are $22.5 \ cm.$

(1)

\text{Area}=\sqrt{30(30-15)(30-22.5)(30-22.5)} (=159.0990258…)

(1)

159

(1)

cm^2

(1)

Learning checklist

You have now learned how to:

Recognise different types of triangles

Solve problems involving the angles of a triangle

Solve problems involving the perimeter of a triangle

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.