GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
ArithmeticThis topic is relevant for:

Factors
Here we will learn about factors, including recognising factors, commutativity, how to systematically find all factor pairs of a number, and solving problems using factors.
There are also factors worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are factors?
Factors are numbers that will divide into an integer (a whole number) with no remainder.
Factors are always integers and can sometimes be called divisors. Every integer has at least \bf{2} factors.
If an integer has only two factors, it is a prime number.
For example, the factors of 5 are 1 and 5.
Step-by-step guide: Prime numbers
If an integer has an odd number of factors, it is a square number.
For example, the factors of 4 are 1, 2, and 4. This is because one factor is repeated.
Step-by-step guide: Square numbers
A factor pair consists of two numbers that are factors of another number and make that number when they are multiplied together.
For example, the factor pairs of 12 are,
\begin{aligned} &1\times{12}\\\\ &2\times{6}\\\\ &3\times{4} \end{aligned}To find all of the factors of any integer, we write out all of the factor pairs in order.
Factor pairs have a commutative property such that you can switch the order of the calculation and the calculation remains the same: 2\times{3}=3\times{2}.
Prime factors are factors of a number that are also prime numbers.
For example, the prime factors of 30=2\times{3}\times{5}.
Step-by-step guide: Prime factors
Once we know what the factors of a number are, we can use these to solve problems involving probability, substitution, completing tables, and area.
We use factors in other areas of maths including factorising algebraic expressions and quadratics, simplifying and equivalent fractions, calculating the highest common factor for a pair of integers, area calculations, and enlargement.
What are factors?

How to list factors
In order to list all of the factor pairs of a number n:
- State the pair \bf{1 \times n.}
- Write the next smallest factor of \bf{n} and calculate its factor pair.
- Repeat until the next factor pair is the same as the previous pair.
- Write out the list of factors for \bf{n.}
Explain how to list factors


Factors worksheet

Get your free factors worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Factors worksheet

Get your free factors worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on factors and multiples
Factors is part of our series of lessons to support revision on factors and multiples and factors, multiples and primes. You may find it helpful to start with the main factors and multiples lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Factors examples
Example 1: listing factors (even number)
List the factors of 24.
- State the pair \bf{1 \times n.}
As n=24, we have the first factor pair 1\times{24}.
2Write the next smallest factor of \bf{n} and calculate its factor pair.
As 24 is an even number, 2 is a factor of 24.
24\div{2}=12so the next factor pair is 2\times{12} .
3Repeat until the next factor pair is the same as the previous pair.
So far we have:
\begin{aligned} &1\times{24}\\\\ &2\times{12}\\ \end{aligned} 24\div{3}=8and so we have the next factor pair 3\times{8} .
24\div{4}=6and so we have the next factor pair 4\times{6} .
24\div{5}=4.8which is a decimal so 5 is not a factor of 24 .
The next factor to try is 6. As factors are commutative,
6\times{4}=4\times{6}which is the same as the previous factor pair.
We have now found all of the factor pairs:
\begin{aligned} &1\times{24}\\\\ &2\times{12}\\\\ &3\times{8}\\\\ &4\times{6} \end{aligned}4Write out the list of factors for \bf{n.}
Reading down the first column of factors, and up the second column, the factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24.
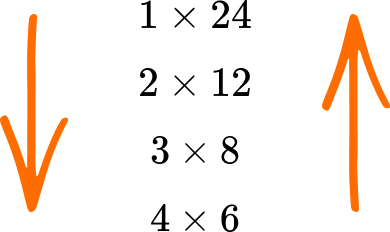
Example 2: listing factors (odd number)
List the factors of 27.
State the pair \bf{1 \times n.}
As n=27, we have the first factor pair 1\times{27}.
Write the next smallest factor of \bf{n} and calculate its factor pair.
As 27 is an odd number, 2 is not a factor of 27.
However, 27\div{3}=9
and so the next factor pair is 3\times{9}.
Repeat until the next factor pair is the same as the previous pair.
So far we have:
\begin{aligned} &1\times{27}\\\\ &3\times{9} \end{aligned}
27 has a remainder when it is divided by 4, 5, 6, 7, or 8.
The next factor to try is 9, but we already know that 3\times{9} is a factor pair and this is the same as 9\times{3}.
We have now found all of the factor pairs:
\begin{aligned}
&1\times{27}\\\\
&3\times{9}
\end{aligned}
Write out the list of factors for \bf{n.}
Reading down the first column of factors, and up the second column, the factors of 27 are: 1, 3, 9, and 27.
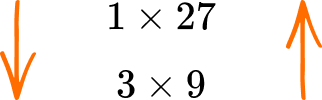
Example 3: listing factors (square number)
List the factors of 36.
State the pair \bf{1 \times n.}
As n=36, we have the first factor pair 1\times{36}.
Write the next smallest factor of \bf{n} and calculate its factor pair.
As 36 is an even number, 2 is a factor of 36.
36\div{2}=18
and so the next factor pair is 2\times{18}.
Repeat until the next factor pair is the same as the previous pair.
So far we have:
\begin{aligned} &1\times{36}\\\\
&2\times{18}
\end{aligned}
36\div{3}=12
and so the next factor pair is 3\times{12} .
36\div{4}=9
and so the next factor pair is 4\times{9} .
36 has a remainder when it is divided by 5 and so 5 is not a factor.
36\div{6}=6
and so the next factor pair is 6\times{6} .
We have reached a repeated factor and so we have found all of the factor pairs for 36:
\begin{aligned}
&1\times{36}\\\\
&2\times{18}\\\\
&3\times{12}\\\\
&4\times{9}\\\\
&6\times{6}
\end{aligned}
Write out the list of factors for \bf{n.}
Reading down the first column of factors, and up the second column, the factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, and 36.
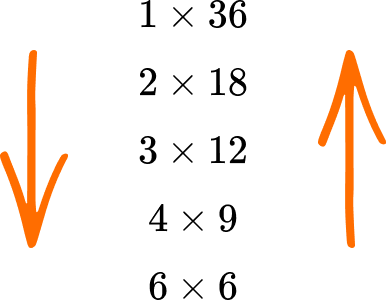
Notice that as we have a repeated factor, we have an odd number of factors in the list above. This can help us determine that 36 is a square number.
Example 4: listing factors (prime number)
List the factors of 7.
State the pair \bf{1 \times n.}
As n=7, we have the first factor pair 1\times{7}.
Write the next smallest factor of \bf{n} and calculate its factor pair.
As 7 is an odd number, 2 is not a factor of 7.
7 has a remainder when it is divided by 2, 3, 4, 5, and 6.
Repeat until the next factor pair is the same as the previous pair.
The next integer to try is 7, which we have already used
(1\times{7}=7\times{1})
and so the only factor pair for the number 7 is 1\times{7}.
Write out the list of factors for \bf{n.}
The factors of 7 are: 1 and 7.
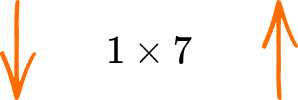
As 7 has only two factors, 1 and itself, 7 is a prime number.
Example 5: listing factors (3 digit number)
List the factors of 200.
State the pair \bf{1 \times n.}
As n=200, we have the first factor pair 1\times{200}.
Write the next smallest factor of \bf{n} and calculate its factor pair.
As 200 is an even number, 2 is a factor of 200.
200\div{2}=100
and so the next factor pair is 2\times{100}.
Repeat until the next factor pair is the same as the previous pair.
So far we have:
\begin{aligned} &1\times{200}\\\\
&2\times{100} \end{aligned}
200 has a remainder when it is divided by 3 and so 3 is not a factor.
200\div{4}=50
and so the next factor pair is 4\times{50}.
200\div{5}=40
and so the next factor pair is 5\times{40}.
200 has a remainder when it is divided by 6 and 7 and so these are not factors of 200.
200\div{8}=25
and so the next factor pair is 8\times{25}.
200 has a remainder when it is divided by 9 and so 9 is not a factor.
200\div{10}=20
and so the next factor pair is 10\times{20} .
200 has a remainder when it is divided by 11, 12, 13, 14, 15, 16, 17, 18, and 19 and so these are not factors of 200.
The next integer to try is 20 but this appears in the previous factor pair
(10\times{20}=20\times{10}).
We have therefore found all of the factor pairs for 200:
\begin{aligned}
&1\times{200}\\\\
&2\times{100}\\\\
&4\times{50}\\\\
&5\times{40}\\\\
&8\times{25}\\\\
&10\times{20}
\end{aligned}
Write out the list of factors for \bf{n.}
Reading down the first column of factors, and up the second column, the factors of 200 are: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, and 200.
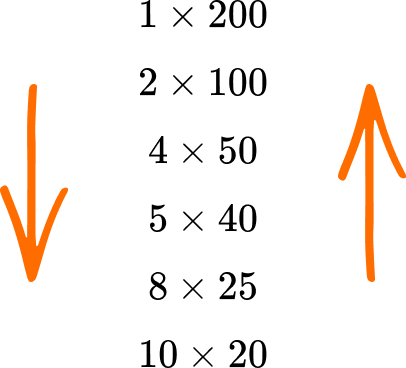
Example 6: listing factors (common factors)
The factors of 6 are 1, 2, 3, and 6. By calculating the factors of 8, determine the common factors of 6 and 8.
State the pair \bf{1 \times n.}
As we want to list the common factors of 6 and 8, we need to find the factors of each of them, and then highlight common factors (the numbers that appear in both lists).
We already have the factors of 6, so we just need to find the factor pairs for 8.
The first factor pair is 1\times{8} .
Write the next smallest factor of \bf{n} and calculate its factor pair.
As 8 is an even number, 2 is a factor of 8.
8\div{2}=4
and so the next factor pair is 2\times{4}.
Repeat until the next factor pair is the same as the previous pair.
8 has a remainder when it is divided by 3.
The next factor to try is 4 and we have already used this in the previous factor pair (2\times{4}=4\times{2}).
We have found all of the factor pairs:
\begin{aligned}
&1\times{8}\\\\
&2\times{4}
\end{aligned}
Write out the list of factors for \bf{n.}
The factors of 8 are: 1, 2, 4, and 8.
The factors of 6 are: 1, 2, 3, and 6.
The common factors of 6 and 8 are: 1 and 2.
Common misconceptions
- Factors and multiples
Factors and multiples are easily mixed up. Remember multiples are the multiplication table, whereas factors are the numbers that go into another number without a remainder.
- Remember \bf{1} and the number itself for factors
All numbers are a factor of themselves and 1 is a factor of every number.
For example, the factors of 6 are: 1, 2, 3, 6 and so 6 is a factor of itself.
Practice factors questions
1. List the factors of 12.

1 and 12, 2 and 6



The factor pairs of 12 are:
\begin{aligned} &1\times{12}\\\\ &2\times{6}\\\\ &3\times{4} \end{aligned}
So the factors of 12 are 1, 2, 3, 4, 6 and 12.
2. List the factors of 15.


3 and 5


The factor pairs of 15 are:
\begin{aligned} &1\times{15}\\\\ &3\times{5} \end{aligned}
So the factors of 15 are 1, 3, 5 and 15.
3. List the factors of 64.

1 and 64, 2 and 32, 8



The factor pairs of 64 are:
\begin{aligned} &1\times{64}\\\\ &2\times{32}\\\\ &4\times{16}\\\\ &8\times{8} \end{aligned}
So the factors of 64 are 1, 2, 4, 8, 16, 32, and 64.
4. List the factors of 17.


1 and 17


The factor pairs of 17 are:
1\times{17}
So the factors of 17 are 1 and 17.
5. List the factors of 120.

12 and 10, 6 and 20, 4 and 30.



The factor pairs of 120 are:
\begin{aligned} &1\times{120}\\\\ &2\times{60}\\\\ &3\times{40}\\\\ &4\times{30}\\\\ &5\times{24}\\\\ &6\times{20}\\\\ &8\times{15}\\\\ &10\times{12} \end{aligned}
So the factors of 120 are: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, and 60.
6. The factors of 10 are 1, 2, 5, and 10. By calculating the factors of 20, determine the common factors of 10 and 20.


1, 2, 5, and 10


The factor pairs of 20 are:
\begin{aligned} &1\times{20}\\\\ &2\times{10}\\\\ &4\times{5} \end{aligned}
So the factors of 20 are: 1, 2, 4, 5, 10, and 20.
The factors of 10 are: 1, 2, 5, and 10.
The common factors of 10 and 20 are: 1, 2, 5, and 10.
Factors GCSE questions
1. Here is a list of numbers:
2, \quad 3, \quad 6, \quad 9, \quad 12, \quad 18, \quad 24
(a) Which numbers are factors of 18?
(b) Which numbers have a common factor of 6?
(c) The product of two numbers is 54. State the two numbers from the list above.
(d) Show that 3 is a factor of 108.
(e) Which number has an odd number of factors?
(5 marks)
(a) 2, 3, 6, 9, 18
(1)
(b) 6, 12, 18, 24
(1)
(c) 6\times{9}
(1)
(d) 108\div{3}=36 and no remainder stated
(1)
(e) 9
(1)
2. Let x and y be two single digit prime numbers where:
- xy is a multiple of 5
- x > y.
(a) List the possible values of x.
(b) Jamal says “ 21 is a prime number as it only has 2 factors, 1 and 21 ”. Is Jamal correct? Explain your answer.
(5 marks)
(a)
5\times{3}=15\textbf{ and }7\times{5}=35
(1)
x=5\text{ and }7(1)
(b)
No
(1)
The factors of 21 are 1, 3, 7, and 21 .
(1)
21 has more than 2 factors and so it is not prime.
(1)
3. A spinner is spun twice. The outcomes are multiplied and written into the sample space diagram below.
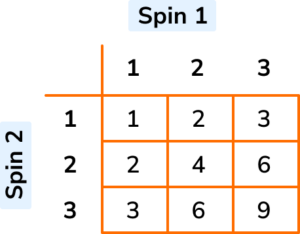
(a) Calculate the probability of getting a factor of 6 after 2 spins.
(b) What is the probability of getting a factor of 8, given that the first spin is a 2?
(4 marks)
(a)
Factors of 6: 1, 2, 3, 6
(1)
\frac{7}{9}(1)
(b)
Factors of 8: 1, 2, 4, 8
(1)
\frac{2}{3}(1)
4. The Venn diagram below shows the two sets A = Factors of 32, and B = Factors of 40 with some values placed.
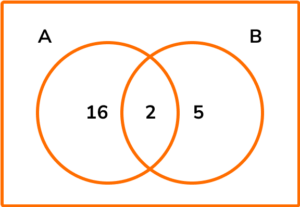
(a) Add all of the factors of 32 and all of the factors of 40 to the Venn diagram.
(b) I pick a factor at random. What is the probability that the factor is also a factor of 12?
(5 marks)
(a)
Factors of 32: 1, 2, 4, 8, 16, 32
(1)
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
(1)
Completed Venn diagram:
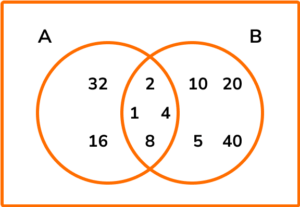
(1)
(b)
Factors of 12: 1, 2, 3, 4, 6, 12
(1)
\frac{3}{10}(1)
Learning checklist
You have now learned how to:
- Use and understand the term factor
- Recognise and use factor pairs and commutativity in mental calculations’
- Identify factors including all factor pairs of a number and common factors of two numbers
- Solve problems involving multiplying and dividing including knowledge of factors
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.